A wheel of radius $r$ rolls without slipping with a speed $v$ on a horizontal road. When it is at a point $A$ on the road, a small jump of mud separates from the wheel at its highest point $B$ and drops at point $C$ on the road. The distance $AC$ will be
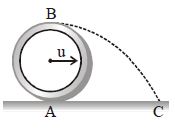
A wheel of radius $r$ rolls without slipping with a speed $v$ on a horizontal road. When it is at a point $A$ on the road, a small jump of mud separates from the wheel at its highest point $B$ and drops at point $C$ on the road. The distance $AC$ will be

- A
$\upsilon \sqrt {\frac{r}{g}} $
- B
$2\upsilon \sqrt {\frac{r}{g}} $
- C
$4\upsilon \sqrt {\frac{r}{g}} $
- D
$\upsilon \sqrt {\frac{3r}{g}} $
Similar Questions
Three thin rods each of length $L$ and mass $M$ are placed along $x, y$ and $z-$ axes is such a way that one end of each of the rods is at the origin. The moment of inertia of this system about $z-$ axis is
Three thin rods each of length $L$ and mass $M$ are placed along $x, y$ and $z-$ axes is such a way that one end of each of the rods is at the origin. The moment of inertia of this system about $z-$ axis is
A spherical uniform body of radius $R$, mass $M$ and moment of inertia $I$ rolls down (without slipping) on an inclined plane making an angle $\theta $ with the horizontal. Then its acceleration is
A spherical uniform body of radius $R$, mass $M$ and moment of inertia $I$ rolls down (without slipping) on an inclined plane making an angle $\theta $ with the horizontal. Then its acceleration is
A disc of mass $M$ and radius $R$ rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is $v,$ the height to which the disc will rise will be
A disc of mass $M$ and radius $R$ rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is $v,$ the height to which the disc will rise will be
A carpenter has constructed a toy as shown in the adjoining figure. If the density of the material of the sphere is $12$ $times$ that of the cone, the position of the centre of mass of the toy is given by
A carpenter has constructed a toy as shown in the adjoining figure. If the density of the material of the sphere is $12$ $times$ that of the cone, the position of the centre of mass of the toy is given by
A cockroach of mass $\frac {M}{2}$ is start moving, with velocity $V$ on the circumference of a disc of mass $'M'$ and $'R',$ what will be angular velocity of disc?
A cockroach of mass $\frac {M}{2}$ is start moving, with velocity $V$ on the circumference of a disc of mass $'M'$ and $'R',$ what will be angular velocity of disc?
