If two glass plates have water between them and are separated by very small distance (see figure), it is very difficult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise to lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is $R$ and surface tension of water is $T$ then the pressure in water between the plates is lower by
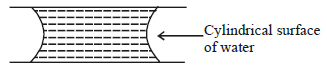
If two glass plates have water between them and are separated by very small distance (see figure), it is very difficult to pull them apart. It is because the water in between forms cylindrical surface on the side that gives rise to lower pressure in the water in comparison to atmosphere. If the radius of the cylindrical surface is $R$ and surface tension of water is $T$ then the pressure in water between the plates is lower by

- A
$\frac{2T}{R}$
- B
$\frac{4T}{R}$
- C
$\frac{T}{4R}$
- D
$\frac{T}{R}$
Similar Questions
The volume of an air bubble becomes three times as it rises from the bottom of a lake to its surface. Assuming atmospheric pressure to be $75\, cm$ of $Hg$ and the density of water to be $1/10 $ of the density of mercury, the depth of the lake is ....... $m$
The volume of an air bubble becomes three times as it rises from the bottom of a lake to its surface. Assuming atmospheric pressure to be $75\, cm$ of $Hg$ and the density of water to be $1/10 $ of the density of mercury, the depth of the lake is ....... $m$
The surface tension of soap solution is $25 \times {10^{ - 3}}\,N{m^{ - 1}}$. The excess pressure inside a soap bubble of diameter $1 \,cm$ is ....... $Pa$
The surface tension of soap solution is $25 \times {10^{ - 3}}\,N{m^{ - 1}}$. The excess pressure inside a soap bubble of diameter $1 \,cm$ is ....... $Pa$
- [AIIMS 1987]
A spherical soap bubble has in ternal pressure $P_0$ and radius $r_0$ and is in equilibrium in an enclosure with pressure ${P_1} = \frac{{8{P_0}}}{9}$ . The enclosure is gradually evacuated . Assuming temperature and surface tension of soap bubble to be fixed find the value of $\frac{{{\rm{final\,\, radius}}}}{{{\rm{initial\,\, radius}}}}$ of soap bubble
A spherical soap bubble has in ternal pressure $P_0$ and radius $r_0$ and is in equilibrium in an enclosure with pressure ${P_1} = \frac{{8{P_0}}}{9}$ . The enclosure is gradually evacuated . Assuming temperature and surface tension of soap bubble to be fixed find the value of $\frac{{{\rm{final\,\, radius}}}}{{{\rm{initial\,\, radius}}}}$ of soap bubble
When two soap bubbles of radii $a$ and $b ( b > a )$ coalesce, the radius of curvature of common surface is
When two soap bubbles of radii $a$ and $b ( b > a )$ coalesce, the radius of curvature of common surface is
- [JEE MAIN 2021]
Consider the following two statement $A$ and $B$, and identify the correct choice in the given answers
$A :$ The excess pressure inside a small liquid drop is more than that of a big drop.
$B :$ As the aeroplane moves fast on the runway the pressure is more on the upper surface of its wings and less on the bottom surface of the wings.
Consider the following two statement $A$ and $B$, and identify the correct choice in the given answers
$A :$ The excess pressure inside a small liquid drop is more than that of a big drop.
$B :$ As the aeroplane moves fast on the runway the pressure is more on the upper surface of its wings and less on the bottom surface of the wings.
