Three alternating voltage sources $V_1$ = $3 sin \omega t $ volt , $V_2= 5 sin(\omega t + \phi _1)$ volt and $V_3 = 5 sin(\omega t -\phi_2 )$ volt connected across a resistance $R= \sqrt {\frac{7}{3}} \Omega $ as shown in the figure (where $ \phi_1$ and $ \phi_2$ corresponds to $30^o $ and $127^o $ respectively). Find the peak current (in Amp) through the resistor
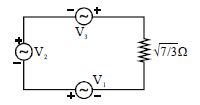
Three alternating voltage sources $V_1$ = $3 sin \omega t $ volt , $V_2= 5 sin(\omega t + \phi _1)$ volt and $V_3 = 5 sin(\omega t -\phi_2 )$ volt connected across a resistance $R= \sqrt {\frac{7}{3}} \Omega $ as shown in the figure (where $ \phi_1$ and $ \phi_2$ corresponds to $30^o $ and $127^o $ respectively). Find the peak current (in Amp) through the resistor

- A
$3$
- B
$4$
- C
$5$
- D
$6$
Similar Questions
An alternating current is given by the equation $i=i_{1} \sin \omega t+i_{2} \cos \omega t$. The rms current will be
An alternating current is given by the equation $i=i_{1} \sin \omega t+i_{2} \cos \omega t$. The rms current will be
- [JEE MAIN 2021]
The $r.m.s.$ value of an ac of $50\,Hz$ is $10\,amp$ . The time taken by the alternating current in reaching from zero to maximum value and the peak value of current will be
The $r.m.s.$ value of an ac of $50\,Hz$ is $10\,amp$ . The time taken by the alternating current in reaching from zero to maximum value and the peak value of current will be
A small signal voltage $V(t) = V_0\,\, sin \omega \,t$ is applied across an ideal capacitor $C$
A small signal voltage $V(t) = V_0\,\, sin \omega \,t$ is applied across an ideal capacitor $C$
- [NEET 2016]
Write the common meaning of voltage.
Write the common meaning of voltage.
In a certain circuit current changes with time according to $i = 2\sqrt t .$ r.m.s. value of current between $t = 2$ to $t = 4s$ will be
In a certain circuit current changes with time according to $i = 2\sqrt t .$ r.m.s. value of current between $t = 2$ to $t = 4s$ will be
