Two stones are thrown up vertically and simultaneously but with different speeds. Which graph correctly represents the time variation of their relative positions $\Delta x$.Assume that stones do not bounce after hitting ground.
Two stones are thrown up vertically and simultaneously but with different speeds. Which graph correctly represents the time variation of their relative positions $\Delta x$.Assume that stones do not bounce after hitting ground.
- A
- B
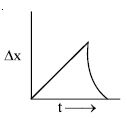
- C
- D
Similar Questions
The height $y$ and the distance $x$ along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by $y = (8t - 5{t^2})$ meter and $x = 6t\, meter$, where $t$ is in second. the angle with the horizontal at which the projectile was projected is
The height $y$ and the distance $x$ along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by $y = (8t - 5{t^2})$ meter and $x = 6t\, meter$, where $t$ is in second. the angle with the horizontal at which the projectile was projected is
A particle moves in the $xy$ -plane with velocity $u_x = 8t -2$ and $u_y = 2$. If it passes through the point $(14, 4)$ at $t = 2\, s$, the equation of its path is
A particle moves in the $xy$ -plane with velocity $u_x = 8t -2$ and $u_y = 2$. If it passes through the point $(14, 4)$ at $t = 2\, s$, the equation of its path is
A boy walks uniformally along the sides of a rectangular park of size $400\, m × 300\, m$, starting from one corner to the other corner diagonally opposite. Which of the following statement is incorrect
Give examples of one dimensional, two dimensional and three dimensional motion.
Give examples of one dimensional, two dimensional and three dimensional motion.
If position time graph of a particle is sine curve as shown, what will be its velocity-time graph.
If position time graph of a particle is sine curve as shown, what will be its velocity-time graph.