A ball is thrown horizontally from a height with a certain initial velocity at time $t=0$. The ball bounces repeatedly from the ground with the coefficient of restitution less than $1$ as shown below. Neglecting air resistance and taking the upward direction as positive, which figure qualitatively depicts the vertical component of the ball's velocity $v_y$ as a function of time $t$ ?

A ball is thrown horizontally from a height with a certain initial velocity at time $t=0$. The ball bounces repeatedly from the ground with the coefficient of restitution less than $1$ as shown below. Neglecting air resistance and taking the upward direction as positive, which figure qualitatively depicts the vertical component of the ball's velocity $v_y$ as a function of time $t$ ?

- [KVPY 2013]
- A
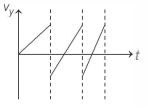
- B

- C

- D

Similar Questions
A body $A,$ of mass $m=0.1\; kg$ has an initial velocity of $3 \hat{\mathrm{i}}\; \mathrm{ms}^{-1} .$ It collides elastically with another body, $\mathrm{B}$ of the same mass which has an initial velocity of $5 \hat{\mathrm{j}} \;\mathrm{ms}^{-1}$. After collision. A moves with a velocity $\overline{\mathrm{v}}=4(\hat{\mathrm{i}}+\hat{\mathrm{j}})$. The energy of $\mathrm{B}$ after collision is written as $\frac{\mathrm{x}}{10} \;\mathrm{J}$ The value of $x$ is
A body $A,$ of mass $m=0.1\; kg$ has an initial velocity of $3 \hat{\mathrm{i}}\; \mathrm{ms}^{-1} .$ It collides elastically with another body, $\mathrm{B}$ of the same mass which has an initial velocity of $5 \hat{\mathrm{j}} \;\mathrm{ms}^{-1}$. After collision. A moves with a velocity $\overline{\mathrm{v}}=4(\hat{\mathrm{i}}+\hat{\mathrm{j}})$. The energy of $\mathrm{B}$ after collision is written as $\frac{\mathrm{x}}{10} \;\mathrm{J}$ The value of $x$ is
- [JEE MAIN 2020]
A heavy steel ball of mass greater than $1\, kg$ moving with a speed of 2$m\,{\sec ^{ - 1}}$collides head on with a stationary ping-pong ball of mass less than $0.1\, gm$. The collision is elastic. After the collision the ping-pong ball moves approximately with speed ......... $m\,{\sec ^{ - 1}}$
A heavy steel ball of mass greater than $1\, kg$ moving with a speed of 2$m\,{\sec ^{ - 1}}$collides head on with a stationary ping-pong ball of mass less than $0.1\, gm$. The collision is elastic. After the collision the ping-pong ball moves approximately with speed ......... $m\,{\sec ^{ - 1}}$
Particle $A$ makes a perfectly elastic collision with another particle $B$ at rest. They fly apart in opposite direction with equal speeds. If their masses are $m_A$ and $m_B$ respectively, then
Particle $A$ makes a perfectly elastic collision with another particle $B$ at rest. They fly apart in opposite direction with equal speeds. If their masses are $m_A$ and $m_B$ respectively, then
A sphere of mass $m $ moving with a constant velocity $u$ hits another stationary sphere of the same mass. If $e$ is the coefficient of restitution, then the ratio of the velocity of two spheres after collision will be
A sphere of mass $m $ moving with a constant velocity $u$ hits another stationary sphere of the same mass. If $e$ is the coefficient of restitution, then the ratio of the velocity of two spheres after collision will be
Four smooth steel balls of equal mass at rest are free to move along a straight line without friction. The first ball is given a velocity of $0.4 \,m/s$. It collides head on with the second elastically, the second one similarly with the third and so on. The velocity of the last ball is .......... $m/s$
Four smooth steel balls of equal mass at rest are free to move along a straight line without friction. The first ball is given a velocity of $0.4 \,m/s$. It collides head on with the second elastically, the second one similarly with the third and so on. The velocity of the last ball is .......... $m/s$
