Explain supplementary quantities and their unit of $SI$ system.

There are two supplementary quantities of $SI$ system.

$(1)$ Plane angle $d \theta$ $(2)$ Solid angle $d \Omega$

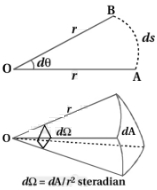
$(1)$ Plane angle $d \theta$ : Ratio of arc of circle and radius of circle is called Plane angle $(d \theta)$

From figure plane angle $d \theta=\frac{\operatorname{arc}}{\text { radius }}=\frac{\mathrm{AB}}{r}=\frac{d s}{r}$

Plane angle subtended at centre by arc of circle having length equal to radius is called $1$ radian. It is represented as rad. Maximum value of plane angle is $2 \pi \mathrm{rad}$.

If $\mathrm{AB}=r$ then, $\theta=1 \mathrm{rad}$.

$\left[1^{\circ}=\frac{\pi}{180} \mathrm{rad}\right]$ and $\left[1 \mathrm{rad}=\frac{180}{\pi}\right.$ degree $]$

$(2)$ Solid angle $d \Omega:$ Angle subtended by area $(\Delta \mathrm{A})$ on spherical surface with centre of sphere is called solid angle $d \Omega$

$d \Omega=d \mathrm{~A} / r^{2}$ steradian

From figure,

Solid angle $d \Omega=\frac{\text { area }}{(\text { radius })^{2}}=\frac{\Delta \mathrm{A}}{r^{2}}$

Maximum value of solid angle is $4 \pi$

Angle subtended on $1 \mathrm{~m}^{2}$ area on sphere of $1 \mathrm{~m}$ radius is called $1$ steradian. Its symbol is $\mathrm{Sr}$.

If $\Delta \mathrm{A}=1 \mathrm{~m}^{2}$ and $r=1 \mathrm{~m}$ then $\Omega=1 \mathrm{Sr}$