એક છોકરી $5\,ms^{-1}$ ની ઝડપથી ઉત્તર દિશામાં સાઇકલ ચલાવે છે જો તેની ઝડપ વધારીને $10\,ms^{-1}$ કરે તો તેને વરસાદ શિરોલંબ સાથે $45^o$ ના ખૂણે પડતો દેખાય છે, તો વરસાદની ઝડપ કેટલી છે ? જમીન પરના અવલોકનકારને વરસાદ પડવાની દિશા કઈ દેખાશે ? 

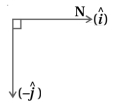
ઉતર દિશામાંનો એકમ સદિશ $\hat{i}$ અને અધોદિશામાંનો એકમ સદિશ $-\hat{j}$ લેતા,

વરસાદનાં ટિપાનો વેગ $\overrightarrow{v_{r}}=a \hat{i}+b \hat{j}$

પ્રથમ કિસ્સો :

છોકરીનો વેગ $\overrightarrow{v_{g}}=5 i\,m\,s ^{-1}$

છોકરીની સાપેક્ષે ટીપાંનો વેગ, $\vec{v}_{r g}=\vec{v}_{r}-\vec{v}_{g}$

$=(a \hat{i}+b \hat{j})-5 \hat{i}$

$=(a-5) \hat{i}+b \hat{j}$

પણ ટીપું અધોદિશામાં પડે છે, તેથી $a-5=0 \Rightarrow \therefore a=5$....(1)

બીજો કિસ્સો:

$\overrightarrow{v_{g}}=10 \hat{i} m s ^{-1}$

$\therefore$ છોકરીની સાપેક્ષે ટીપાંનો વેગ $\vec{v}_{r g}=\overrightarrow{v_{r}}-\overrightarrow{v_{g}}=(a \hat{i}+b \hat{j})-5 \hat{i}=(a-10) \hat{i}+b \hat{j}$

ટીપું ઊર્ધ્વદિશા સાથે $45^{\circ}$ ના ખૂણો પડતું દેખાય છે.

તેથી $\tan 45^{\circ}=\frac{b}{a-10}$

$\therefore 1=\frac{b}{a-10}$

$\therefore a-10=b$

$\therefore 5-10=b$ (પરિણામ $(1)$ પરથી)

$\therefore b=-5$$.............2$

$\therefore$ વરસાદ (ટિપાનો)નો વેગ $\overrightarrow{v_{r}}=a \hat{i}+b \hat{j}=5 \hat{i}-5 \hat{j} \quad$ (પરિણામ $(1)$ અને $(2)$ પરથી)

અને મૂલ્ય એટલે ઝડપ $=\sqrt{(5)^{2}+(-5)^{2}}=\sqrt{25+25}=\sqrt{50}$

$\therefore v_{r}=5 \sqrt{2} m s ^{-1}$