Two blocks $'A$' and $'B'$ each of mass $'m'$ are placed on a smooth horizontal surface. Two horizontal force $F$ and $2F$ are applied on the $2$ blocks $'A'$ and $'B'$ respectively as shown in figure. The block $A$ does not slide on block $B$. Then the normal reaction acting between the two blocks is
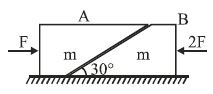
Two blocks $'A$' and $'B'$ each of mass $'m'$ are placed on a smooth horizontal surface. Two horizontal force $F$ and $2F$ are applied on the $2$ blocks $'A'$ and $'B'$ respectively as shown in figure. The block $A$ does not slide on block $B$. Then the normal reaction acting between the two blocks is

- A
$F$
- B
$F/2$
- C
$\frac{F}{{\sqrt 3 }}$
- D
$3\,F$
Similar Questions
A block $B$ is placed on block $A$. The mass of block $B$ is less than the mass of block $A$. Friction exists between the blocks, whereas the ground on which the block $A$ is placed is taken to be smooth. $A$ horizontal force $F$, increasing linearly with time begins to act on $B$. The acceleration ${a_A}$ and ${a_B}$ of blocks $A$ and $B$ respectively are plotted against $t$. The correctly plotted graph is
A block $B$ is placed on block $A$. The mass of block $B$ is less than the mass of block $A$. Friction exists between the blocks, whereas the ground on which the block $A$ is placed is taken to be smooth. $A$ horizontal force $F$, increasing linearly with time begins to act on $B$. The acceleration ${a_A}$ and ${a_B}$ of blocks $A$ and $B$ respectively are plotted against $t$. The correctly plotted graph is
Two blocks of mass $M_1 = 20\,kg$ and $M_2 = 12\,kg$ are connected by a metal rod of mass $8\,kg.$ The system is pulled vertically up by applying a force of $480\,N$ as shown. The tension at the mid-point of the rod is ........ $N$
Two blocks of mass $M_1 = 20\,kg$ and $M_2 = 12\,kg$ are connected by a metal rod of mass $8\,kg.$ The system is pulled vertically up by applying a force of $480\,N$ as shown. The tension at the mid-point of the rod is ........ $N$
- [JEE MAIN 2013]
A block of mass $m$ is placed on a smooth inclined wedge $ABC$ of inclination $\theta$ as shown in the figure. The wedge is given an acceleration $a$ towards the right. The relation between $a$ and $\theta$ for the block to remain stationary on the wedge is
A block of mass $m$ is placed on a smooth inclined wedge $ABC$ of inclination $\theta$ as shown in the figure. The wedge is given an acceleration $a$ towards the right. The relation between $a$ and $\theta$ for the block to remain stationary on the wedge is
- [NEET 2018]
Four blocks are connected as shown in the fig. on a horizontal frictionless surface of $m_1 = m_2 = m_3 = m_4$ then $T_3/T_4$ will be
Four blocks are connected as shown in the fig. on a horizontal frictionless surface of $m_1 = m_2 = m_3 = m_4$ then $T_3/T_4$ will be
Two bodies of masses $m_{1}=5\,kg$ and $m _{2}=3\,kg$ are connected by a light string going over a smooth light pulley on a smooth inclined plane as shown in the figure. The system is at rest. The force exerted by the inclined plane on the body of mass $m _{1}$ will be$....N$ [Take $g=10\,ms ^{-2}$ ]
Two bodies of masses $m_{1}=5\,kg$ and $m _{2}=3\,kg$ are connected by a light string going over a smooth light pulley on a smooth inclined plane as shown in the figure. The system is at rest. The force exerted by the inclined plane on the body of mass $m _{1}$ will be$....N$ [Take $g=10\,ms ^{-2}$ ]
- [JEE MAIN 2022]
