$4\, kg$ का कोई गुटका एक क्षैतिज समतल पर रखा है (चित्र)। समतल को धीरे-धीरे तब तक आनत किया जाता है जब तक क्षेतिज से किसी कोण $\theta=15^{\circ}$ पर वह गुटका सरकना आरंभ नहीं कर देता । पृष्ठ और गुटके के बीच स्थेतिक घर्षण गुणांक क्या है ?
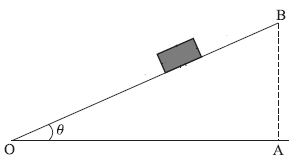
$4\, kg$ का कोई गुटका एक क्षैतिज समतल पर रखा है (चित्र)। समतल को धीरे-धीरे तब तक आनत किया जाता है जब तक क्षेतिज से किसी कोण $\theta=15^{\circ}$ पर वह गुटका सरकना आरंभ नहीं कर देता । पृष्ठ और गुटके के बीच स्थेतिक घर्षण गुणांक क्या है ?
Answer The forces acting on a block of mass $m$ at rest on an inclined plane are $(i)$ the weight mg acting vertically downwards $(ii)$ the normal force $N$ of the plane on the block, and $(iii)$ the static frictional force $f_{ s }$ opposing the impending motion. In equilibrium, the resultant of these forces must be zero. Resolving the weight $m g$ along the two directions shown, we have
$m g \sin \theta=f_{s}, \quad m g \cos \theta=N$
As $\theta$ increases, the self-adjusting frictional force
$f_{ s }$ increases until at $\theta=\theta_{\max ^{\prime}} f_{ s }$ achieves its
maximum value, $\left(f_{s}\right)_{\max }=\mu_{s} N$
Therefore.
$\tan \theta_{\max }=\mu_{s}$ or $\theta_{\max }=\tan ^{-1} \mu_{s}$
When $\theta$ becomes Just a little more than $\theta_{\max }$. there is a small net force on the block and it begins to slide. Note that $\theta_{\max }$ depends only on
$\mu_{ s }$ and $1 s$ independent of the mass of the block.
For $\quad \theta_{\max }=15^{\circ}$
$\mu_{s}=\tan 15^{\circ}$
$=0.27$
Similar Questions
$m$ द्रव्यमान का एक गुटका खुरदरे क्षैतिज तल पर रखा है। इस पर क्षैतिज दिशा में $P$ बल तथा ऊध्र्वाधर से $\theta $ दिशा में $Q$ बल आरोपित किया गया है। यदि गुटका संतुलन की अवस्था में हो, तो गुटके व पृष्ठ के मध्य घर्षण गुणांक होगा
$1000 \,kg$ द्रव्यमान का एक सैनिक वाहन $10 \,m/s$ के वेग से गतिमान है और इस पर इंजिन द्वारा आगे की दिशा में $1000\, N$ का बल एवं घर्षण के कारण $500 \,N$ का अवमंदक बल कार्यरत् है। $10 \,sec$ पश्चात इसका वेग ........... $m/s$ होगा
$1000 \,kg$ द्रव्यमान का एक सैनिक वाहन $10 \,m/s$ के वेग से गतिमान है और इस पर इंजिन द्वारा आगे की दिशा में $1000\, N$ का बल एवं घर्षण के कारण $500 \,N$ का अवमंदक बल कार्यरत् है। $10 \,sec$ पश्चात इसका वेग ........... $m/s$ होगा
एक खुरदुरे क्षैतिज फर्श पर एक भारी बक्से को खींचा जाता है। ऐसा करने के लिये, व्यक्ति $A$ को क्षैतिज से $30^{\circ}$ कोण पर धक्का लगाना पड़ता है और न्यूनतम बल $F _{ A }$ की आवश्यकता होती हैं जब कि व्यक्ति $B$ को क्षैतिज से $60^{\circ}$ कोण पर खींचना होता है और न्यूनतम बल $F _{ B }$ की आवश्यकता होती हैं। यदि फर्श एवं बक्से के बीच घर्षण गुणाँक $\frac{\sqrt{3}}{5}$ हैं, तब अनुपात $\frac{ F _{ A }}{ F _{ B }}$ हैं :
एक खुरदुरे क्षैतिज फर्श पर एक भारी बक्से को खींचा जाता है। ऐसा करने के लिये, व्यक्ति $A$ को क्षैतिज से $30^{\circ}$ कोण पर धक्का लगाना पड़ता है और न्यूनतम बल $F _{ A }$ की आवश्यकता होती हैं जब कि व्यक्ति $B$ को क्षैतिज से $60^{\circ}$ कोण पर खींचना होता है और न्यूनतम बल $F _{ B }$ की आवश्यकता होती हैं। यदि फर्श एवं बक्से के बीच घर्षण गुणाँक $\frac{\sqrt{3}}{5}$ हैं, तब अनुपात $\frac{ F _{ A }}{ F _{ B }}$ हैं :
- [JEE MAIN 2014]
$m$ द्रव्यमान की एक वस्तु क्षैतिज सतह पर रखी है। वस्तु तथा सतह के बीच घर्षण गुणांक का मान $\mu .$ है। यदि द्रव्यमान को चित्र में दर्शाए अनुसार खींचा जाए, तब वस्तु तथा सतह के बीच सीमान्त घर्षण का मान होगा
$m$ द्रव्यमान की एक वस्तु क्षैतिज सतह पर रखी है। वस्तु तथा सतह के बीच घर्षण गुणांक का मान $\mu .$ है। यदि द्रव्यमान को चित्र में दर्शाए अनुसार खींचा जाए, तब वस्तु तथा सतह के बीच सीमान्त घर्षण का मान होगा
$1 \;kg$ द्रव्यमान का कोई पिण्ड किसी क्षैतिज पष्ठ जिसका स्थैतिक घर्षण गुणांक $\frac{1}{\sqrt{3}}$ है पर विराम में स्थित है। यदि कोई निम्नतम संभव बल $FN$ लगाकर इस पिण्ड को गति कराना चाहता है तो $F$ का मान $\dots$ होगा। (निकटतम पूर्णांक तक पूर्णांकित) $[ g =10\; ms ^{-2}$ लीजिए $]$
$1 \;kg$ द्रव्यमान का कोई पिण्ड किसी क्षैतिज पष्ठ जिसका स्थैतिक घर्षण गुणांक $\frac{1}{\sqrt{3}}$ है पर विराम में स्थित है। यदि कोई निम्नतम संभव बल $FN$ लगाकर इस पिण्ड को गति कराना चाहता है तो $F$ का मान $\dots$ होगा। (निकटतम पूर्णांक तक पूर्णांकित) $[ g =10\; ms ^{-2}$ लीजिए $]$
- [JEE MAIN 2021]