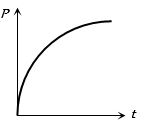
A soap bubble is blown with the help of a mechanical pump at the mouth of a tube. The pump produces a certain increase per minute in the volume of the bubble, irrespective of its internal pressure. The graph between the pressure inside the soap bubble and time $t$ will be-

In capillary pressure below the curved surface of water will be

The pressure at the bottom of a tank containing a liquid does not depend on

A spherical drop of water has radius $1\, mm$ If surface tension of water is $70 \times {10^{ - 3}}\,N/m$ difference of pressures between inside and out side of the spherical drop is ........ $N/{m^{ - 2}}$

A spherical soap bubble of radius $3\,cm$ is formed inside another spherical soap bubble of radius $6\,cm$. If the internal pressure of the smaller bubble of radius $3\,cm$ in the above system is equal to the internal pressure of the another single soap bubble of radius $r\,cm$. The value of $r$ is.......

Formation of bubble are in Column - $\mathrm{I}$ and pressure difference between them are given in Column - $\mathrm{II}$. Match them appropriately.