A vertical glass capillary tube of radius $r$ open at both ends contains some water (surface tension $T$ and density $\rho$ ). If $L$ be the length of the water column, then:
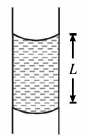
A vertical glass capillary tube of radius $r$ open at both ends contains some water (surface tension $T$ and density $\rho$ ). If $L$ be the length of the water column, then:

- A
$L=\frac{4 T}{r \rho g}$
- B
$L=\frac{2 T}{r \rho g}$
- C
$L=\frac{T}{4 r \rho g}$
- D
$L=\frac{T}{2 r \rho g}$
Similar Questions
A liquid column of height $0.04 \mathrm{~cm}$ balances excess pressure of soap bubble of certain radius. If density of liquid is $8 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ and surface tension of soap solution is $0.28 \mathrm{Nm}^{-1}$, then diameter of the soap bubble is . . . . . . .. . $\mathrm{cm}$.
$\text { (if } g=10 \mathrm{~ms}^{-2} \text { ) }$
A liquid column of height $0.04 \mathrm{~cm}$ balances excess pressure of soap bubble of certain radius. If density of liquid is $8 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ and surface tension of soap solution is $0.28 \mathrm{Nm}^{-1}$, then diameter of the soap bubble is . . . . . . .. . $\mathrm{cm}$.
$\text { (if } g=10 \mathrm{~ms}^{-2} \text { ) }$
- [JEE MAIN 2024]
Two bubbles $A$ and $B$ $(r_A > r_B)$ are joined through a narrow tube. Then
Two bubbles $A$ and $B$ $(r_A > r_B)$ are joined through a narrow tube. Then
Air (density $\rho$ ) is being blown on a soap film (surface tension $T$ ) by a pipe of radius $R$ with its opening right next to the film. The film is deformed and a bubble detaches from the film when the shape of the deformed surface is a hemisphere. Given that the dynamic pressure on the film due to the air blown at speed $v$ is $\frac{1}{2} \rho v^{2}$, the speed at which the bubble formed is
Air (density $\rho$ ) is being blown on a soap film (surface tension $T$ ) by a pipe of radius $R$ with its opening right next to the film. The film is deformed and a bubble detaches from the film when the shape of the deformed surface is a hemisphere. Given that the dynamic pressure on the film due to the air blown at speed $v$ is $\frac{1}{2} \rho v^{2}$, the speed at which the bubble formed is
- [KVPY 2018]
A soap bubble, blown by a mechanical pump at the mouth of a tube, increases in volume, with time, at a constant rate. The graph that correctly depicts the time dependence of pressure inside the bubble is given by
A soap bubble, blown by a mechanical pump at the mouth of a tube, increases in volume, with time, at a constant rate. The graph that correctly depicts the time dependence of pressure inside the bubble is given by
- [JEE MAIN 2019]
Derive the formula for excess of pressure (pressure difference) inside the drop and bubble.
Derive the formula for excess of pressure (pressure difference) inside the drop and bubble.
