Figure shows $(x,\, t)$, $(y,\, t)$ diagram of a particle moving in $2-$ dimensions.
If the particle has a mass of $500\,g$, find the force (direction and magnitude) acting on the particle.
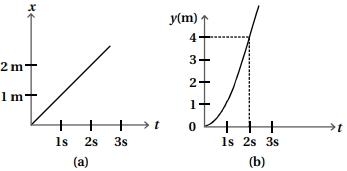
Figure shows $(x,\, t)$, $(y,\, t)$ diagram of a particle moving in $2-$ dimensions.
If the particle has a mass of $500\,g$, find the force (direction and magnitude) acting on the particle.

From figure $(a)$,
Velocity $v=\frac{\Delta x}{\Delta t}=\frac{2-0}{2-0}=1 \mathrm{~m} / \mathrm{s}$ constant velocity.
$\Delta v=0, a_{x}=0$
From figure (b),
Mathematical relation $y=t^{2}$
$v =\frac{d y}{d t}=2 t$
$a=\frac{d v}{d y}=2(1)=2$
$\mathrm{~F}_{x} &=m a_{x} \mid \quad \mathrm{F}_{y}=m a_{y}$
$=0.5(0)$
$=0$
Resultant force,
$\mathrm{F} &=\sqrt{\mathrm{F}_{x}^{2}+\mathrm{F}_{y}^{2}}$
$=\sqrt{0^{2}+1^{2}}$
$=1 \mathrm{~N}$
Similar Questions
When body is at rest or it is in uniform motion, no force act on it.
When body is at rest or it is in uniform motion, no force act on it.
Two masses $M$ and $m$ are connected by a weightless string. They are pulled by a force $F$ on a frictionless horizontal surface., the acceleration of mass $m$ is
Two masses $M$ and $m$ are connected by a weightless string. They are pulled by a force $F$ on a frictionless horizontal surface., the acceleration of mass $m$ is
Describe Galileo’s experiment of inclined plane regarding motion.
Describe Galileo’s experiment of inclined plane regarding motion.
If an inclined plane is made slowly horizontal by reducing its inclination with horizontal, the component of weight parallel to the plane of block resting on the inclined plane
If an inclined plane is made slowly horizontal by reducing its inclination with horizontal, the component of weight parallel to the plane of block resting on the inclined plane
Explain primary concept of force.
Explain primary concept of force.


