આકૃતિમાં દર્શાવ્યા પ્રમાણે બે ઓછા અંતરે રહેલ ગ્લાસની પ્લેટની વચ્ચે પાણી છે.તેમને જુદી પાડવા મુશ્કેલ છે કારણ કે તેમની વચ્ચે રહેલ પાણી બાજુ પરથી નળાકાર સપાટી બનાવે છે જેના કારણે ત્યાં વાતાવરણ કરતાં ઓછું દબાણ ઉત્પન્ન થાય છે.જો નળાકાર સપાટીની ત્રિજ્યા $R$ અને પાણીનું પૃષ્ઠતાણ $T$ હોય તો બંન્ને પ્લેટ વચ્ચે રહેલ પાણીનું દબાણ કેટલું ઘટે?
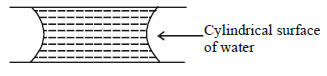
આકૃતિમાં દર્શાવ્યા પ્રમાણે બે ઓછા અંતરે રહેલ ગ્લાસની પ્લેટની વચ્ચે પાણી છે.તેમને જુદી પાડવા મુશ્કેલ છે કારણ કે તેમની વચ્ચે રહેલ પાણી બાજુ પરથી નળાકાર સપાટી બનાવે છે જેના કારણે ત્યાં વાતાવરણ કરતાં ઓછું દબાણ ઉત્પન્ન થાય છે.જો નળાકાર સપાટીની ત્રિજ્યા $R$ અને પાણીનું પૃષ્ઠતાણ $T$ હોય તો બંન્ને પ્લેટ વચ્ચે રહેલ પાણીનું દબાણ કેટલું ઘટે?

- [JEE MAIN 2015]
- A
$\frac {T}{R}$
- B
$\frac {4T}{R}$
- C
$\frac {T}{4R}$
- D
$\frac {2T}{R}$
Similar Questions
પ્રવાહીના બુંદ અને પરપોટા માટે દબાણના તફાવતનું સમીકરણ તારવો.
પ્રવાહીના બુંદ અને પરપોટા માટે દબાણના તફાવતનું સમીકરણ તારવો.
એક ઊભી ગ્લાસની કેપિલરી ટ્યુબની ત્રિજ્યા $r$ છે અને બંને છેડેથી ખુલ્લી છે. અને અમુક પાણીનો જથ્થો ધરાવે છે. ($T$ પૃષ્ઠતાણ અને $\rho$ ઘનતા). જો $L$ એ પાણીના સ્તંભની લંબાઈ હોય તો $.......$
એક ઊભી ગ્લાસની કેપિલરી ટ્યુબની ત્રિજ્યા $r$ છે અને બંને છેડેથી ખુલ્લી છે. અને અમુક પાણીનો જથ્થો ધરાવે છે. ($T$ પૃષ્ઠતાણ અને $\rho$ ઘનતા). જો $L$ એ પાણીના સ્તંભની લંબાઈ હોય તો $.......$
પાણીમાં રહેલા પરપોટાનું દબાણ $P_1$. છે,સમાન ત્રિજયા ધરાવતા ટીપાંનું દબાણ $P_2$ છે,તો
પાણીમાં રહેલા પરપોટાનું દબાણ $P_1$. છે,સમાન ત્રિજયા ધરાવતા ટીપાંનું દબાણ $P_2$ છે,તો
જો સાબુના પરપોટાનું વિસ્તરણ થાય તો, પરપોટાની અંદરનું દબાણ
જો સાબુના પરપોટાનું વિસ્તરણ થાય તો, પરપોટાની અંદરનું દબાણ
- [NEET 2022]
વિધાન : નાના ટીપાં મોટા ટીપાં કરતાં વધારે પ્રતિબળનો વિરોધ કરે.
કારણ : ટીપાની અંદરનું દબાણ તેની સપાટીના ક્ષેત્રફળના સમપ્રમાણમાં હોય
વિધાન : નાના ટીપાં મોટા ટીપાં કરતાં વધારે પ્રતિબળનો વિરોધ કરે.
કારણ : ટીપાની અંદરનું દબાણ તેની સપાટીના ક્ષેત્રફળના સમપ્રમાણમાં હોય
- [AIIMS 2004]
