एक $R$ त्रिज्या के गोले में समान घनत्व $\rho$ का आवेश वितरित है। यदि इस गोले से $\frac{ R }{2}$ त्रिज्या का एक गोला काटकर चित्रानुसार निकाल दिया जाय तो बचे हुए भाग के कारण बिन्दु ओं $A$ तथा $B$ पर विधुत क्षेत्र (क्रमशः $\overrightarrow{ E }_{ A }$ तथा $\overrightarrow{ E }_{ B }$ ) के मान का अनुपात $\frac{\left|\overrightarrow{ E }_{ A }\right|}{\left|\overrightarrow{ E }_{ B }\right|}$ होगा।
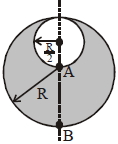
एक $R$ त्रिज्या के गोले में समान घनत्व $\rho$ का आवेश वितरित है। यदि इस गोले से $\frac{ R }{2}$ त्रिज्या का एक गोला काटकर चित्रानुसार निकाल दिया जाय तो बचे हुए भाग के कारण बिन्दु ओं $A$ तथा $B$ पर विधुत क्षेत्र (क्रमशः $\overrightarrow{ E }_{ A }$ तथा $\overrightarrow{ E }_{ B }$ ) के मान का अनुपात $\frac{\left|\overrightarrow{ E }_{ A }\right|}{\left|\overrightarrow{ E }_{ B }\right|}$ होगा।

- [JEE MAIN 2020]
- A
$\frac{18}{54}$
- B
$\frac{21}{34}$
- C
$\frac{17}{54}$
- D
$\frac{18}{34}$
Similar Questions
एक अनन्त लम्बा रैखिक आवेश $2\,cm$ की दूरी पर $7.182 \times {10^8}\,N/C$ का विद्युत क्षेत्र उत्पन कर रहा है। रेखीय आवेश घनत्व होगा
एक अनन्त लम्बा रैखिक आवेश $2\,cm$ की दूरी पर $7.182 \times {10^8}\,N/C$ का विद्युत क्षेत्र उत्पन कर रहा है। रेखीय आवेश घनत्व होगा
अपरिमित लम्बाई और $R$ त्रिज्या के एक ठोस बेलन पर एक समान आयतन-आवेश-घनत्व $\rho$ है। इसमें $R / 2$ त्रिज्या एक खोखला गोलीय-कोष बेलन के अक्ष पर केन्द्रित है (चित्र देखिये)$।।$ अक्ष से $2 \ R$ दूरी पर स्थित बिन्दु $P$ पर विधुत $\frac{23 p }{16 k \varepsilon_0}$ से दिया जाता है। तब $k$ का मान क्या है ?
अपरिमित लम्बाई और $R$ त्रिज्या के एक ठोस बेलन पर एक समान आयतन-आवेश-घनत्व $\rho$ है। इसमें $R / 2$ त्रिज्या एक खोखला गोलीय-कोष बेलन के अक्ष पर केन्द्रित है (चित्र देखिये)$।।$ अक्ष से $2 \ R$ दूरी पर स्थित बिन्दु $P$ पर विधुत $\frac{23 p }{16 k \varepsilon_0}$ से दिया जाता है। तब $k$ का मान क्या है ?
- [IIT 2012]
त्रिज्या $R$ के एक समान गोलीय आयतन आवेश वितरण (uniform spherical volume charge distribution) को लीजिए। निम्नलिखित में से कौन सा ग्राफ गोलक (sphere) के मध्य से $r$ की दूरी पर विद्युत क्षेत्र (electric field) $E$ का परिमाण (magnitude) निरूपित करता है ?
त्रिज्या $R$ के एक समान गोलीय आयतन आवेश वितरण (uniform spherical volume charge distribution) को लीजिए। निम्नलिखित में से कौन सा ग्राफ गोलक (sphere) के मध्य से $r$ की दूरी पर विद्युत क्षेत्र (electric field) $E$ का परिमाण (magnitude) निरूपित करता है ?
- [KVPY 2010]
एक गोलीय सममिति में वितरित आवेश के परिवर्तनशील आवेश घनत्व को निम्न समीकरण द्वारा निरूपित किया गया है।
$\rho(r)=\left\{\begin{array}{ll}\rho_0\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{array}\right.$
जहाँ, $r ( r < R )$ केन्द्र $O$ से दूरी है, (चित्र में दर्शाये अनुसार) $P$ बिन्दू पर विद्युत क्षेत्र का मान होगा :
एक गोलीय सममिति में वितरित आवेश के परिवर्तनशील आवेश घनत्व को निम्न समीकरण द्वारा निरूपित किया गया है।
$\rho(r)=\left\{\begin{array}{ll}\rho_0\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{array}\right.$
जहाँ, $r ( r < R )$ केन्द्र $O$ से दूरी है, (चित्र में दर्शाये अनुसार) $P$ बिन्दू पर विद्युत क्षेत्र का मान होगा :
- [JEE MAIN 2022]
एकसमान रूप से आवेशित गोले की त्रिज्या $R$ है। इसके केन्द्र से $r$ दूरी एवं उत्पन्न विद्युत क्षेत्र के बीच सही ग्राफीय निरूपण होगा
एकसमान रूप से आवेशित गोले की त्रिज्या $R$ है। इसके केन्द्र से $r$ दूरी एवं उत्पन्न विद्युत क्षेत्र के बीच सही ग्राफीय निरूपण होगा
- [AIIMS 2004]
